How to calculate row spacing on a tilted surface?

If you want a Short Answer, here it is:
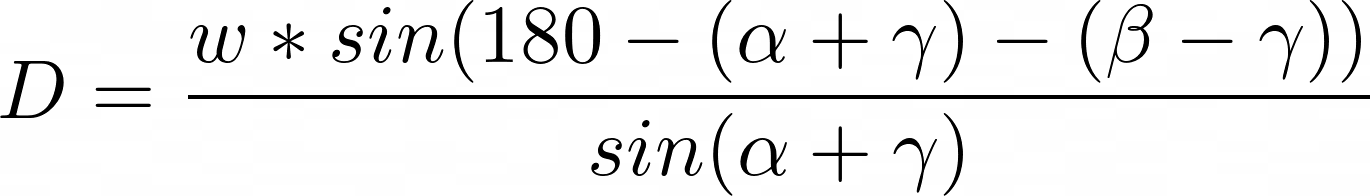
Now, let me explain it.
Recently I was working on a project related to Solar PV and the plan was to design a system with the panels on a tilted roof. However, the tilt was too low (10°) and we wanted to add additional tilt to panels (+25°). In this way, the question arises: how to calculate the row distance to avoid self-shading? Of course, it's possible to do it using modern software like PV*SOL, Helioscope, or SketchUp, but I was interested in the manual ways to make those calculations.
When it comes to the ground-mounted system, the formula to calculate the row distance is following:
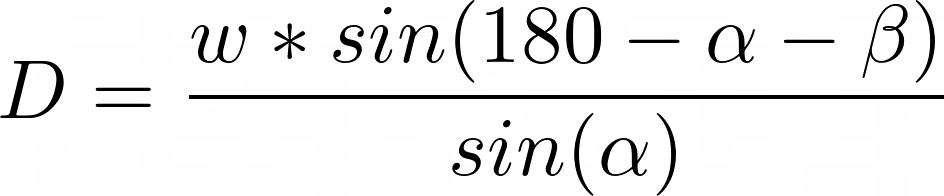
where α is an Elevation angle of the sun at solar noon on December 21 (or June 21 in the southern part of the world), wis the width of the panel, β is the tilt of the PV panels, and D is the distance between the PV panels (end-to-end). This equation is based on the simple formulas from trigonometry (all of them are taken from the right triangle equations). For the countries that are located on the same latitude as Azerbaijan (40°), the formula can sometimes be further simplified to D = 2.5 w. Let's better define them with the diagram/image:
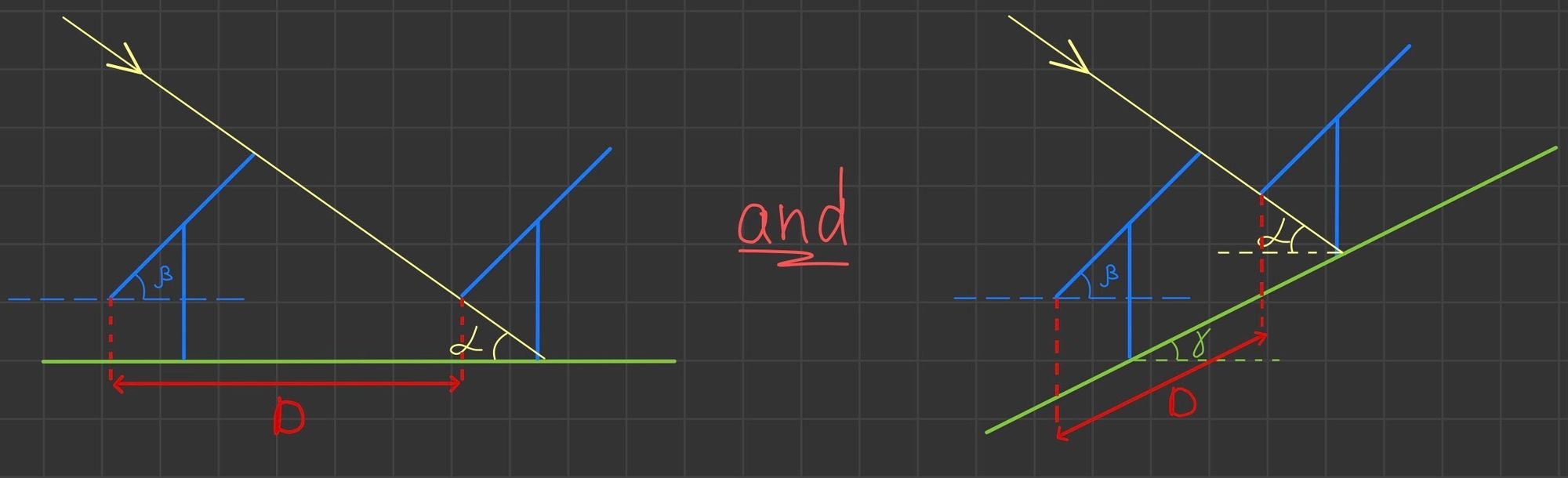
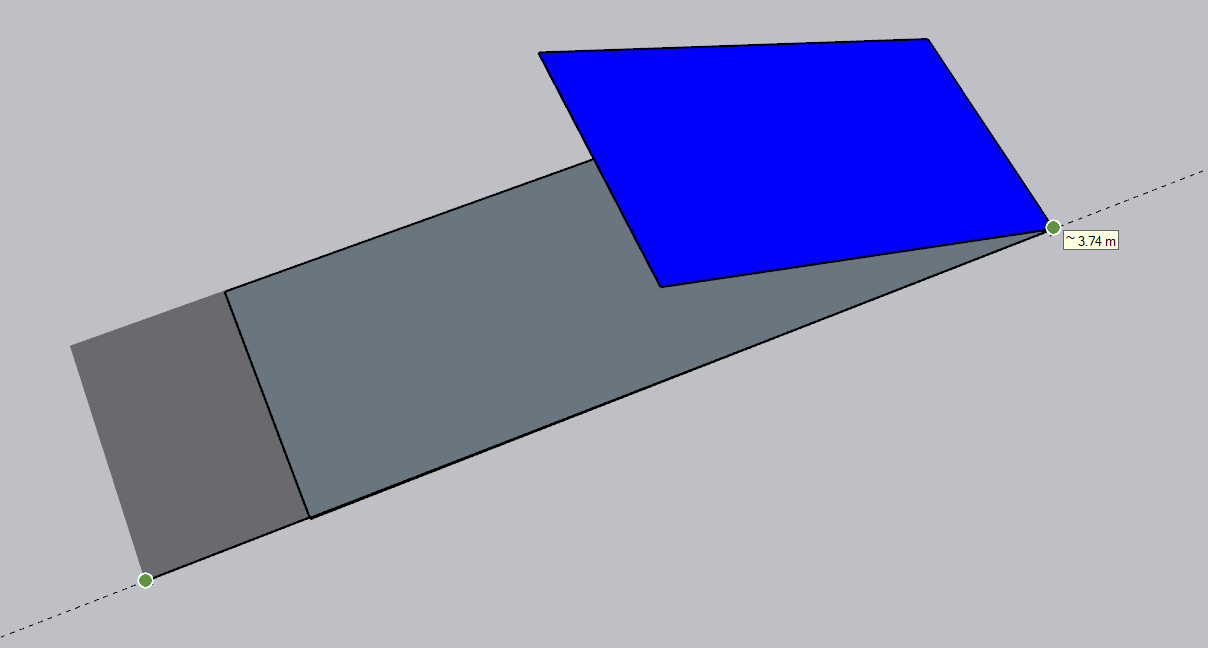
Here, we can see one more variable: γ, which is a tilt of the surface.
We cannot apply the first formula for the panels that are located on the tilted surface, because the shadow on the tilted surface will not be as long as on the horizontal one. For that reason, we need another equation.
But first, let's check whether the first equation is giving the right results. We could use math to justify the equation, but it's more fun and visual if we show it in SketchUp. So, I built a simple plane with different tilts of panels and different surface tilts.
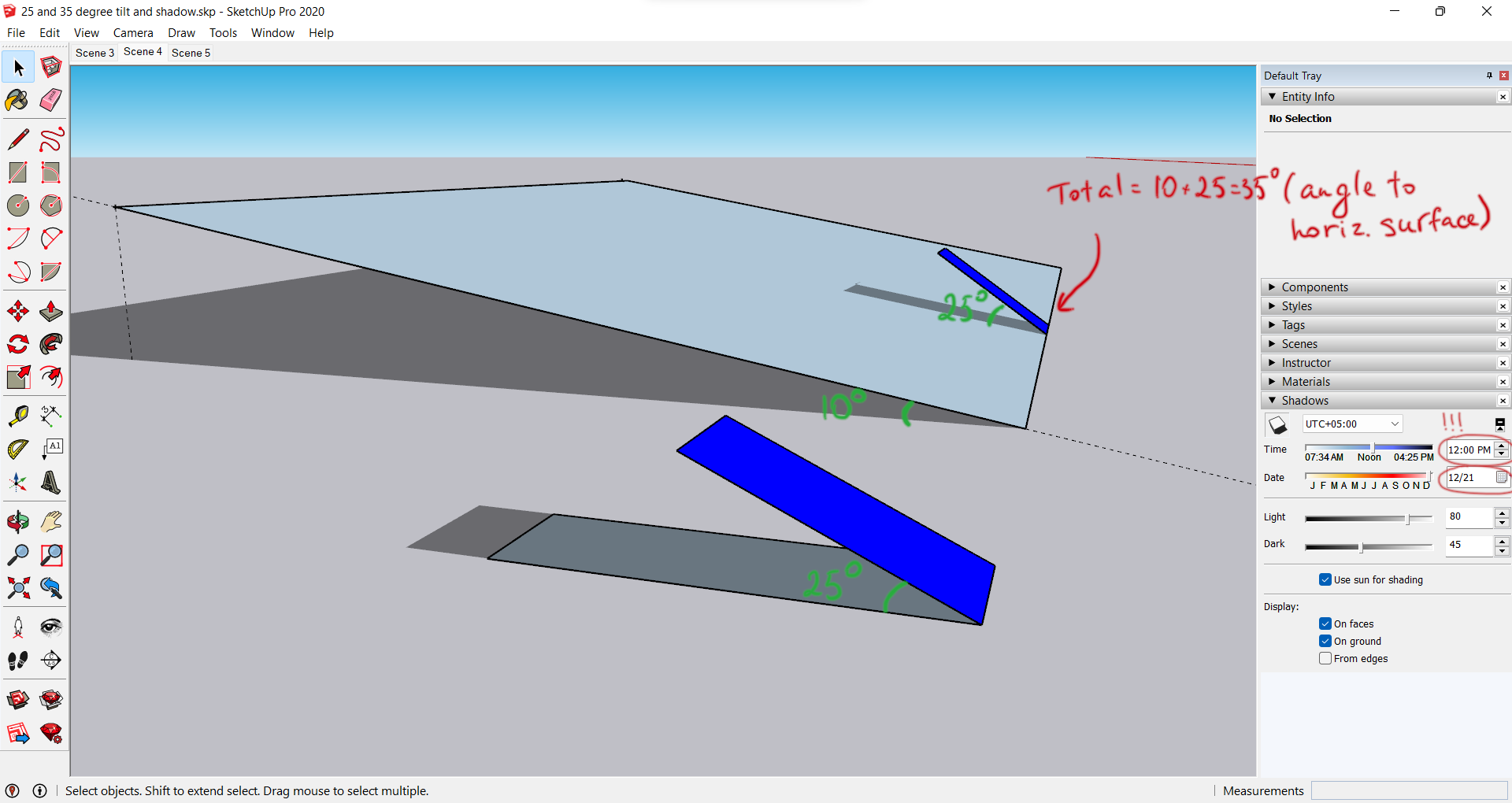
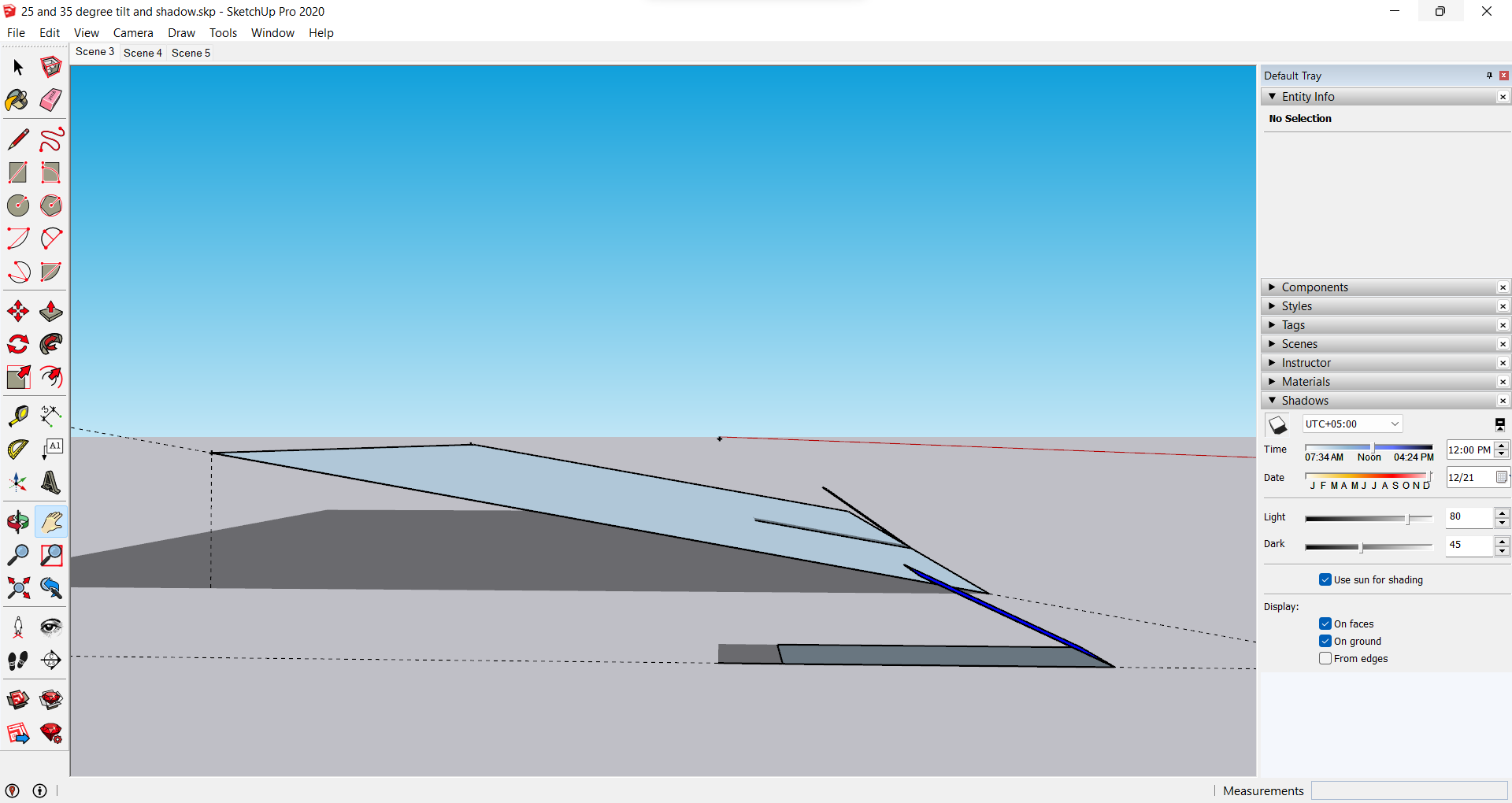
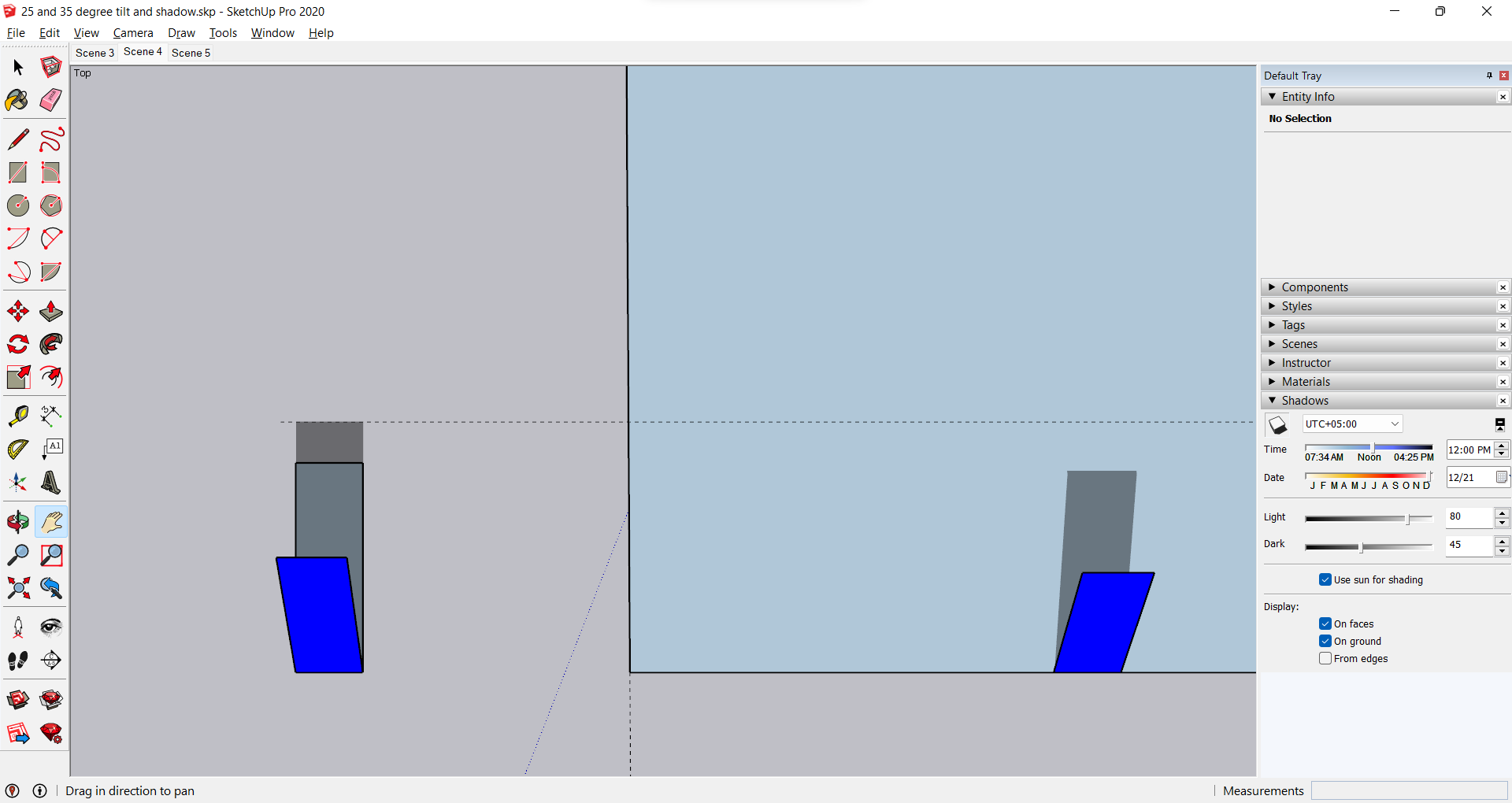
We can clearly see that the shadow on a tilted surface is shorter. But this is a simulation... Let's check whether the initial equation really works. To validate the first equation, let's look at the panel that is "installed" on the flat ground. Here are the giver parameters:
- w = 2 m
- β = 25°
- γ = 0°
- α = 23.7°
- Latitude: 42.8°
- Day of the year: December, 21
- Time of the day: 12:00 (noon)
We calculate the row distance for December 21, because this is the day of the winter solstice (the shortest day of the year), so the sun is in the lowest position, which makes the longest shadows in comparison to other days. As for the time of the day, we take noon, because we expect the largest insolation at that time of the day, and we should have no self-shadowing at that time.
Alpha is calculated using the following equation: α = 90° - 23.5° - Latitude. If you ask where the number "-23.5°" comes from, it is the largest Earth tilt that happens on December 21. We need to consider it and the latitude of the place to calculate the Elevation angle of the sun.
So, if you "run the numbers" using the equation for ground-mounted panels, you get the answer of D = 3.7381...
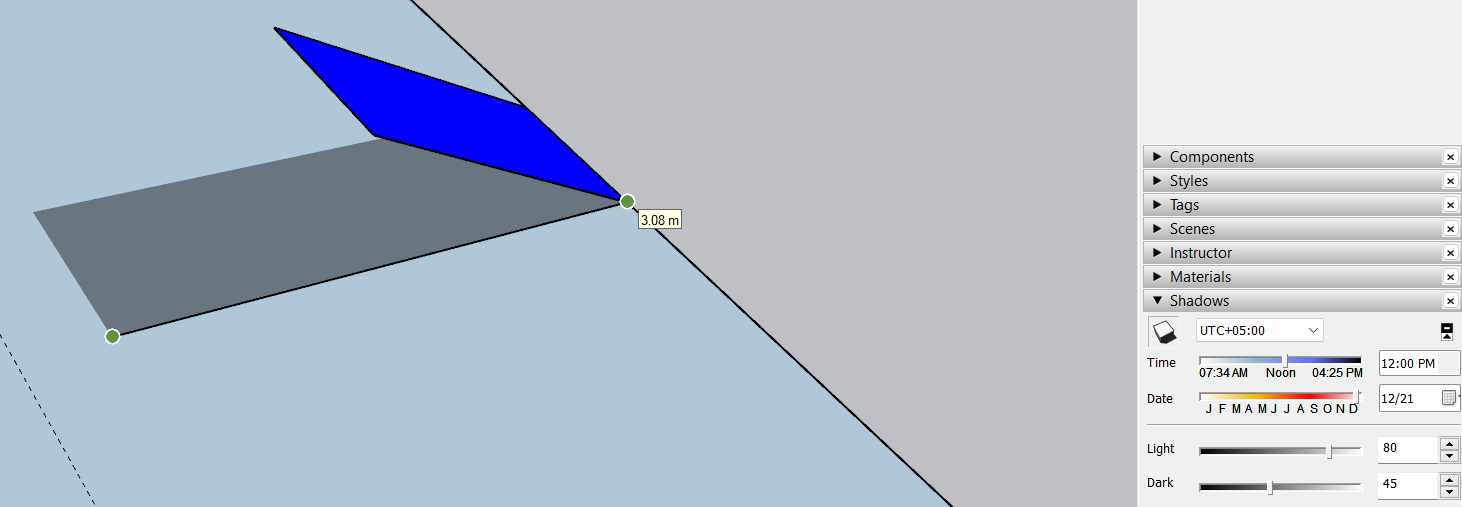
The SketchUp results show the same results:
This shows that our equation works, and shadow simulation gives the same results.
So, now, it's time to modify the equation we have to calculate the row distance, but on the tilted surface. And the answer is simple: we need to get two new angles. To get a new β, we subtract the γ from β, and to get new α we add γ to α. With that in mind, the updated equation looks like this:
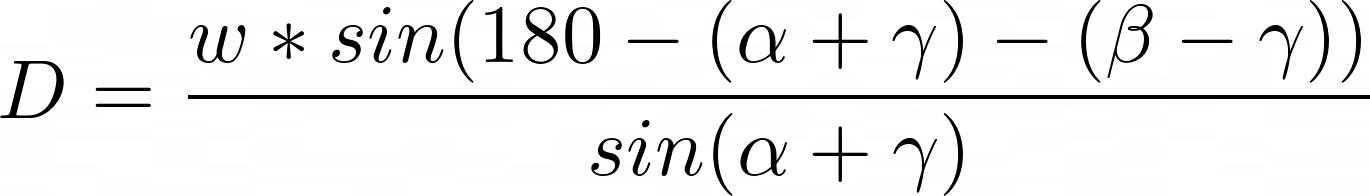
Now, let's run the numbers again and validate the results in SketchUp. The given variables are the same as in the first simulation/calculation, with these differences:
- β = 35° (I changed it to 35° to get 25° on a tilted surface at the end)
- γ = 10°
With this, we get D = 3.07999...
And the results are validated by SketchUp.
So, if you ever need to manually calculate the minimum row spacing for PV panels on a tilted surface, you know what equation to use.
What software/tool do you use for shadow analysis? Let me know in the comment section below.